English
Français
Listen to the rhythm of the sound by turning your speakers on or by wearing your headphones and push the play button (>). What you’re hearing is known as a Shepard scale.
You’ll likely notice that the scale appears to be continually moving downwards, but only so far. Think of it as an auditory equivalent to the old-fashioned styled barber pole. So just how is this possible with a sound pattern?
The Paradox of Shepard Scales
It’s no easy task to describe what’s going on in Shepard scales, but if your intellectual curiosity has been melodiously tweaked, then keep on reading!
Sounds that we think of as having a “pitch” such as a note played on a musical instrument or a singing voice are typically complex signals that are composed of energy that vibrates at many varying frequency levels.
As an example, when a middle “C” is being sung, the sound produced contains energy not only at the “middle C pitch” that one hears (approx. 260Hz), but also across the range of harmonic frequencies: 520, 780, 1040 and so on – that is, multiple units of 260Hz.
To determine which note is being sung, our auditory system uses this spacing, and not just the fact that 260HZ is the lowest frequency level. In actual fact, even if you erased all of the energy emitted at 260HZ, you would still be hearing the note as a middle C.
Shepard tones, as you have just heard, are uniquely different and consist of harmonics that are an octave apart. Each Shepard Tone is comprised only of octaves of the fundamental frequency, meaning that each successive frequency is twice that of the last one, so the ratios are 1, 2, 4, 8, 16, etc. (In the case of a “C,” there might be 130, 260, 520, 1040 Hz, etc. instead of the constant spacing of 260 Hz).
So although the presence of all of these frequencies tell us that it's some kind of a “C,” we can't use that constant 260 Hz spacing to determine exactly which “C” it is.
Making things even trickier, in Shepard tones the volume is set higher at a constant frequency that is unrelated to the pitch of the note (ex: 368 Hz). Tapering off to near silence at the higher and lower ends of the range, most of its energy are at the harmonics closest to the constant frequency, no matter what note you hear.
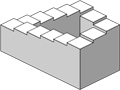These elements make your brain record a seemingly implausible scale: one that constantly descends, and yet does not get any lower. The result we are left with are the musical contours of an "ever-ascending" scale, which is a sort of auditory analog to the ever-ascending staircase visual illusion as you see on the left.
